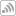Beauty and the ‘triply periodic minimal surface’ beast
“Imagine taking a long piece of wire. Bend it into some shape in space and solder the ends together. You might have some crazy curves. Dip it in dish soap. Pull it out. You probably will have a spanning film on there, some kind of soap film. I study a mathematical model of those things,” said Adam Weyhaupt, assistant professor of mathematics and statistics at SIUE’s College of Arts and Sciences (CAS).
Weyhaupt is interested in a theoretical part of mathematics known as minimal surfaces, which he stated is an expression of efficiency.
“The whole idea of minimal surfaces is an idea of efficiency–what’s a soap film going to do? A soap film, if you put a ring in there and pull it out, it’s not going to have some big finger in it, some big bubble in it,” stated Weyhaupt. “It’s going to be nice and smooth and try to take up as little area as possible. So, it’s this sort of idea of efficiency.”
Weyhaupt is particularly interested in a subset of minimal surfaces know as triply periodic minimal surfaces. Weyhaupt’s website defines the gyroid as a “triply periodic minimal surface that contains no straight lines or planar symmetry curves.” These are minimal surfaces that can be assembled, said Weyhaupt, and are found in many branches of science.
“Chemists and Biologists–which I am not–they care about this because they can find these at the molecular level. So, in certain plastics and rubbers they can find these surfaces. Biologists find these in cellular membranes,” said Weyhaupt. “They care about them that way; I think about them from the theoretical standpoint.”
The gyroid, Weyhaupt’s research interest, is based on work done by Alan Schoen in 1970, according to an article that Weyhaupt will have published soon, which is entitled “What do butterflies, ketchup, microcellular structures and plastics have in common? The gyroid.” Weyhaupt described triply periodic minimal surfaces and its function in its simplest terms.
“It’s possible to build a little piece of these that I can use to repeat and build a bigger surface in space. Just like you can imagine me taking Lego blocks and building some little fundamental piece and then telling you ‘O.K., now hook these [pieces] together in this way’ and you’ll have a line of pieces. ‘Now take that line and hook them together this way,’ and now you will have a sort of a grid of pieces. Now, take that–you can imagine me taking and stacking those grids,” said Weyhaupt. “And then I will have something that will fill up space.”

A 'simple' gyroid (left) and the structure created from assembling the gyroids (right). courtesy of Weyhaupt.
These structures have very practical applications in math, science and engineering, as Weyhaupt stated. Computer chipmakers are very interested in the structures as well.
“You may have heard of nano materials–nano means very small, like 10-9th–so chip makers, for instance, have this idea that wires are too thick and silicone is somehow too thick. If we could build little nano-structures, little tubes made out of carbon or something, then we could cram a lot more stuff on that chip,” said Weyhaupt.
Weyhaupt stated that chip makers believe that it may be possible for these structures to self assemble, at the nano-level.
“One of the things that those guys think is that you can get molecules to self-assemble at the molecular level–so at the nano-scale level–into little gyroids. Understanding this, this might be some sort of a structure that you could get molecules to build themselves into, which means you don’t have to hook these things together, or weld them together. How do you do this at the molecular level?” asked Weyhaupt. “You want to try to get them to assemble themselves. They [chip makers] think that the gyroid is a structure that can assemble itself. It’s somehow naturally nice.”
Weyhaupt stated that his interest in gyroids is less practical and more in terms of the naturally nice form.
“I want to push back against the very notion, of practicality. The argument that I would make is that we study poetry because it is beautiful or maybe it has an emotional impact on people. We study plenty of things that are not immediately practical. They may in fact be practical to someone. They may not be practical now; they may be practical later,” said Weyhaupt.
Even though practical application is important, Weyhaupt stated that he sees an aesthetic beauty in the forms. He said he is interested in math for math’s sake. Mathematics does not always need to be practical in the way that many people understand practical. And that’s ok, according to Weyhaupt.
“I am a theoretical mathematician. So, to me that means that I am interested in understanding the structure of something. It doesn’t have to be for a practical reason. It’s just because–here is an object and I want to understand it. I happen to think that these [structures] are a lot like poetry,” said Weyhaupt. “These are beautiful. If you stare at them long enough, there is something deeply beautiful here, in all of the symmetries.”
Filed Under: Mathematics & Statistics